使用MFC的CDC类绘制三维坐标系及球面函数

发表于 | 分类于

系列链接

概述

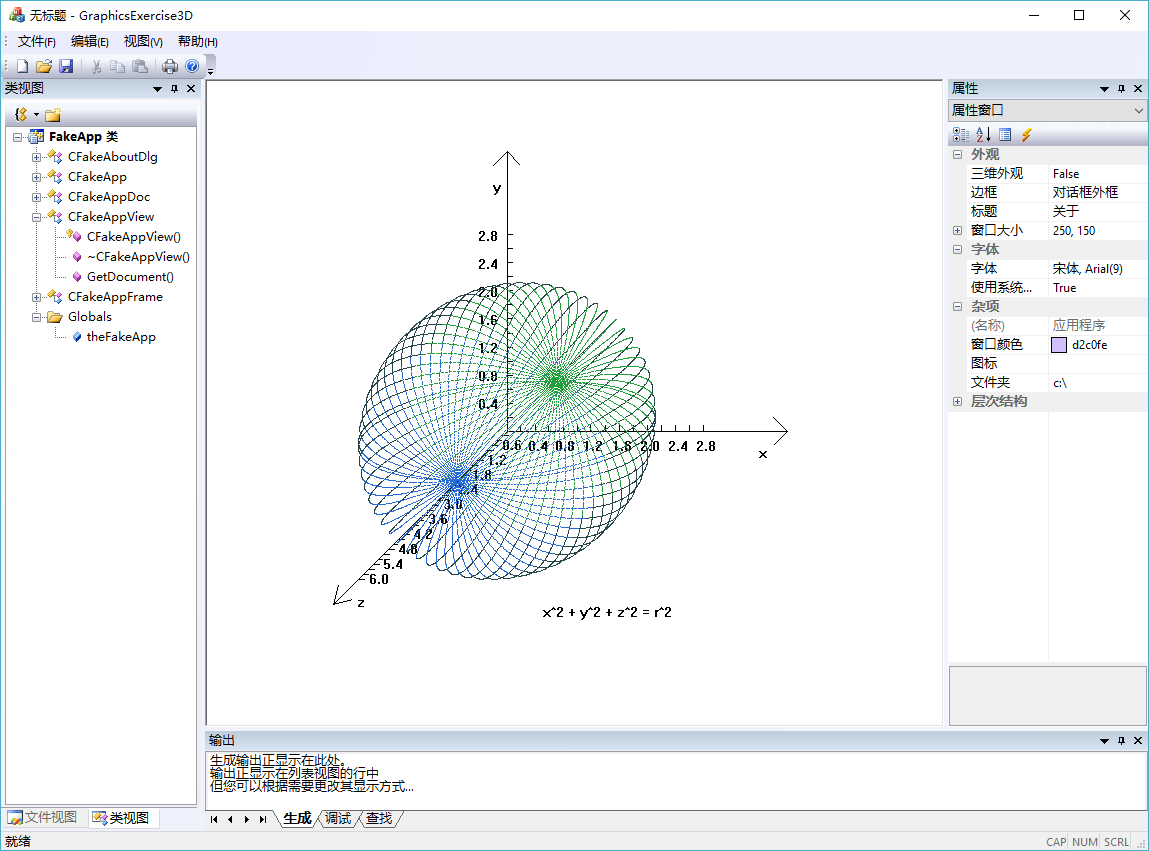
本文使用MFC的CDC类绘制三维坐标系及球面函数。首先计算推导出三维坐标在二维平面显示的坐标变换方程（使用斜二测视图），使用球面的参数方程，然后定义图形缩放比例规模、坐标轴位移，变换坐标系和规模等，最后绘制坐标轴及球面函数。

如果对绘制二维坐标系还不太熟悉可以先看上面系列链接的：使用MFC的CDC类绘制二维坐标系及正余弦函数，本文对二维绘制及绘制函数部分不再赘述。因为二维坐标系的博文已经分模块讲解地比较清楚了，而与三维坐标系的基本思路相同，所以本文大部分直接使用注释讲解。

三维转二维的推导

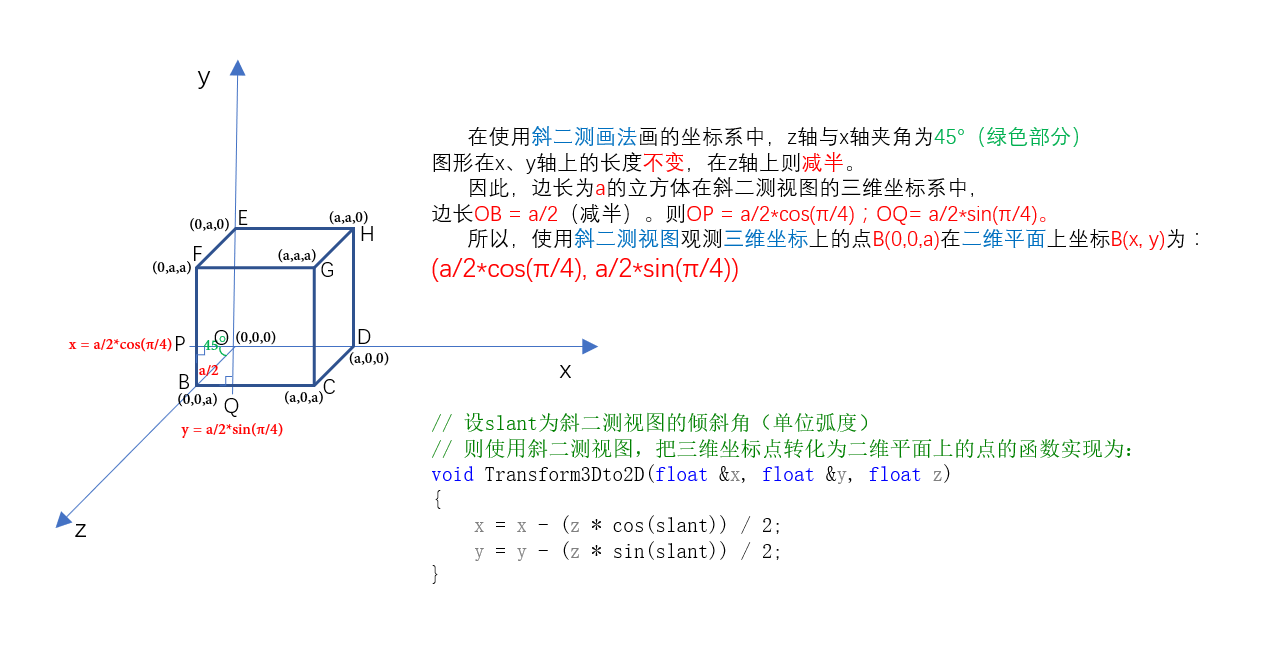
Transform3Dto2D

上图可知，只要使用Transform3Dto2D()函数，即可方便的把三维坐标转化为二维坐标（斜二测视图）。

球面参数方程

在三维空间直角坐标系中，以原点为球心、半径为 r 的球面的方程为 x^2 + y^2 + z^2 = r^2，其参数方程为

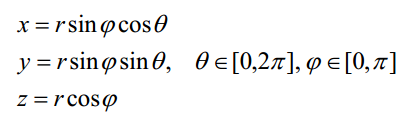
SphericalParameterEquation

新建项目

Visual Studio- 新建项目 - MFC应用程序 - 命名为GraphicsExercise3D - 确定 - 下一步 - 应用程序类型选择单个文档 - 完成

GraphicsExercise3DView.h

在GraphicsExercise3DView.h添加以下内容

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 操作
public:
	void SetScale(int scale);
	void SetTransformOrigin(float transformOriginX, float transformOriginY);
	void SetPlotSphere(float radius, float stepPhi, float stepTheta);
  	void SetSlantRadian(float slant);

	float TransformScale(float num);
	float TransformOriginX(float x);
	float TransformOriginY(float y);
	float TransformOriginScaleX(float x);
	float TransformOriginScaleY(float y);
	void Transform3Dto2D(float &x, float &y, float z);

private:
    int scale;
    float radius, stepPhi, stepTheta, slant, transformOriginX, transformOriginY;

GraphicsExercise3DView.cpp

引入数学函数库

1
#include <math.h>

定义π

1
2
3
#ifndef PI
#define PI 3.14159
#endif // !PI

在构造函数初始化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
CGraphicsExercise3DView::CGraphicsExercise3DView()
{
	// TODO: 在此处添加构造代码

	// 设置斜二测视图倾斜角度（弧度制）
	SetSlantRadian(PI / 4);

	// 设置规模比例
	SetScale(70);

	// 设置坐标系在x、y方向的位移（不改变规模情况下，即移动像素）
	SetTransformOrigin(300, 350);

	// 设置球面半径radius、取样步长stepPhi、stepTheta
	SetPlotSphere(2.0, 0.01, 0.1);
}

设置初始化参数的Set函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 设置规模
void CGraphicsExercise3DView::SetScale(int scale)
{
	this->scale = scale;
}

// 设置坐标系原点在x、y方向的位移（不改变规模情况下，即移动像素）
void CGraphicsExercise3DView::SetTransformOrigin(float transformOriginX, float transformOriginY)
{
	this->transformOriginX = transformOriginX;
	this->transformOriginY = transformOriginY;
}

// 设置球面半径radius、取样步长stepPhi、stepTheta
void CGraphicsExercise3DView::SetPlotSphere(float radius, float stepPhi, float stepTheta)
{
	this->radius = radius;
	this->stepPhi = stepPhi;
	this->stepTheta = stepTheta;
}

// 设置斜二测视图的倾斜角（单位弧度）
void CGraphicsExercise3DView::SetSlantRadian(float slant)
{
	this->slant = slant;
}

坐标及规模变换

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// 变换规模
float CGraphicsExercise3DView::TransformScale(float num)
{
	return num * scale;
}

// 坐标系X轴方向位移
float CGraphicsExercise3DView::TransformOriginX(float x)
{
	return x + transformOriginX / scale;
}

// 坐标系y轴方向位移
float CGraphicsExercise3DView::TransformOriginY(float y)
{
	return y - transformOriginY / scale;
}

// 变换坐标系X和规模
float CGraphicsExercise3DView::TransformOriginScaleX(float x)
{
	return TransformScale(TransformOriginX(x));
}

// 变换坐标系Y和规模
float CGraphicsExercise3DView::TransformOriginScaleY(float y)
{
	return -TransformScale(TransformOriginY(y));
}

三维坐标转化为二维坐标

1
2
3
4
5
6
// 使用斜二测视图，把三维坐标点转化为二维平面上的点
void CGraphicsExercise3DView::Transform3Dto2D(float &x, float &y, float z)
{
	x = x - (z * cos(slant)) / 2;
	y = y - (z * sin(slant)) / 2;
}

绘制坐标轴及函数图形

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
// CGraphicsExercise2View 绘制

void CGraphicsExercise3DView::OnDraw(CDC* pDC)
{
	CGraphicsExercise3DDoc* pDoc = GetDocument();
	ASSERT_VALID(pDoc);
	if (!pDoc)
		return;

	// TODO: 在此处为本机数据添加绘制代码

	float x, y, z;

	// -------------------- 绘制坐标系 -------------------------

	// 坐标x轴
	pDC->MoveTo(TransformOriginScaleX(0), TransformOriginScaleY(0));
	pDC->LineTo(TransformOriginScaleX(radius + 2), TransformOriginScaleY(0));

	// 坐标y轴
	pDC->MoveTo(TransformOriginScaleX(0), TransformOriginScaleY(0));
	pDC->LineTo(TransformOriginScaleX(0), TransformOriginScaleY(radius + 2));

	// 坐标z轴
	x = 0, y = 0;
	Transform3Dto2D(x, y, radius + 5);
	pDC->MoveTo(TransformOriginScaleX(0), TransformOriginScaleY(0));
	pDC->LineTo(TransformOriginScaleX(x), TransformOriginScaleY(y));

	// 坐标x轴的箭头
	pDC->MoveTo(TransformOriginScaleX(radius + 1.8), TransformOriginScaleY(0.2));
	pDC->LineTo(TransformOriginScaleX(radius + 2), TransformOriginScaleY(0));
	pDC->LineTo(TransformOriginScaleX(radius + 1.8), TransformOriginScaleY(-0.2));

	// 坐标y轴的箭头
	pDC->MoveTo(TransformOriginScaleX(-0.2), TransformOriginScaleY(radius + 1.8));
	pDC->LineTo(TransformOriginScaleX(0), TransformOriginScaleY(radius + 2));
	pDC->LineTo(TransformOriginScaleX(0.2), TransformOriginScaleY(radius + 1.8));

	// 坐标z轴的箭头
	x = 0, y = 0.2;
	Transform3Dto2D(x, y, radius + 5 - 0.2);
	pDC->MoveTo(TransformOriginScaleX(x), TransformOriginScaleY(y));
	x = 0, y = 0;
	Transform3Dto2D(x, y, radius + 5);
	pDC->LineTo(TransformOriginScaleX(x), TransformOriginScaleY(y));
	x = 0.2, y = 0;
	Transform3Dto2D(x, y, radius + 5 - 0.2);
	pDC->LineTo(TransformOriginScaleX(x), TransformOriginScaleY(y));

	// -------------------- 绘制刻度线 -------------------------

	// 绘制x轴刻度线
	for (float scaleX = 0.2; scaleX < radius + 1; scaleX += 0.2)
	{
		pDC->MoveTo((int)TransformOriginScaleX(scaleX), (int)TransformOriginScaleY(0));
		pDC->LineTo((int)TransformOriginScaleX(scaleX), (int)TransformOriginScaleY(0.1));
	}

	// 绘制y轴刻度线
	for (float scaleY = 0.2; scaleY <= radius + 1; scaleY += 0.2)
	{
		pDC->MoveTo((int)TransformOriginScaleX(0), (int)TransformOriginScaleY(scaleY));
		pDC->LineTo((int)TransformOriginScaleX(0.1), (int)TransformOriginScaleY(scaleY));
	}

	// 绘制z轴刻度线
	for (float x = 0, y = 0, scaleZ = 0.2; scaleZ <= radius + 4; scaleZ += 0.2, x = 0, y = 0)
	{
		Transform3Dto2D(x, y, scaleZ);
		pDC->MoveTo((int)TransformOriginScaleX(x), (int)TransformOriginScaleY(y));
		pDC->LineTo((int)TransformOriginScaleX(x + 0.1), (int)TransformOriginScaleY(y));
	}


	// -------------------- 绘制文字 -------------------------

	// 绘制x轴的x
	pDC->TextOutW(TransformOriginScaleX(radius + 1.6), TransformOriginScaleY(-0.2), CString("x"));
	// 绘制y轴的y
	pDC->TextOutW(TransformOriginScaleX(-0.2), TransformOriginScaleY(radius + 1.6), CString("y"));
	// 绘制z轴的z
	x = 0.2, y = 0;
	Transform3Dto2D(x, y, radius + 5 - 0.4);
	pDC->TextOutW(TransformOriginScaleX(x), TransformOriginScaleY(y), CString("z"));

	CString s;
	// 绘制x轴刻度文字
	for (float ScaleTextX = 0.4; ScaleTextX < radius + 1; ScaleTextX += 0.4)
	{
		s.Format(_T("%.1f"), ScaleTextX);
		pDC->TextOutW(TransformOriginScaleX(ScaleTextX - 0.1), TransformOriginScaleY(-0.1), s);
	}

	// 绘制y轴刻度文字
	for (float ScaleTextY = 0.4; ScaleTextY <= radius + 1; ScaleTextY += 0.4)
	{
		s.Format(_T("%.1f"), ScaleTextY);
		pDC->TextOutW(TransformOriginScaleX(-0.4), TransformOriginScaleY(ScaleTextY + 0.1), s);
	}

	// 绘制z轴刻度文字
	for (float ScaleTextZ = 0.6; ScaleTextZ <= radius + 4; ScaleTextZ += 0.6)
	{
		s.Format(_T("%.1f"), ScaleTextZ);
		x = 0, y = 0;
		Transform3Dto2D(x, y, ScaleTextZ);
		pDC->TextOutW(TransformOriginScaleX(x + 0.15), TransformOriginScaleY(y + 0.12), s);
	}

	// 绘制函数图的Title
	x = 0, y = 0;
	Transform3Dto2D(x, y, radius + 5);
	pDC->TextOutW(TransformOriginScaleX(x + 3), TransformOriginScaleY(y), CString("x^2 + y^2 + z^2 = r^2"));

	// -------------------- 绘制函数 -------------------------

	// 球面
	float phi, theta;
	for (phi = 0; phi < 2 * PI; phi += stepPhi)
	{
		for (theta = 0; theta < PI; theta += stepTheta)
		{
			x = radius * sin(phi) * cos(theta);
			y = radius * sin(phi) * sin(theta);
			z = radius * cos(phi);

			Transform3Dto2D(x, y, z);

			srand(z);
			pDC->SetPixel(TransformOriginScaleX(x), TransformOriginScaleY(y), RGB(rand() % 255, rand() % 255, rand() % 255));
		}
	}


	//// 三棱锥（测试用）
	//x = 1, y = 0, z = 0;
	//Transform3Dto2D(x, y, z);
	//pDC->MoveTo((int)TransformOriginScaleX(x), (int)TransformOriginScaleY(y));

	//x = 0, y = 1, z = 0;
	//Transform3Dto2D(x, y, z);
	//pDC->LineTo((int)TransformOriginScaleX(x), (int)TransformOriginScaleY(y));

	//x = 0, y = 0, z = 1;
	//Transform3Dto2D(x, y, z);
	//pDC->LineTo((int)TransformOriginScaleX(x), (int)TransformOriginScaleY(y));

	//x = 1, y = 0, z = 0;
	//Transform3Dto2D(x, y, z);
	//pDC->LineTo((int)TransformOriginScaleX(x), (int)TransformOriginScaleY(y));

}

效果图

GraphicsExercise3DCapture